Limites et fonctions continues

Limites et fonctions continues - analyse 1

Accueil | Mathématique | Analyse 1 | cours en ligne

Chapitre 2 : Limites et fonctions continues

1. Notions de fonction
1.1. Définitions

1.2. Opérations sur les fonctions

1.3. Fonctions majorées, minorées, bornées

1.4. Fonctions croissantes, décroissantes

1.5. Parité et périodicité

Interprétation graphique :
– f est paire si et seulement si son graphe est symétrique par rapport à l’axe des ordonnées.
– f est impaire si et seulement si son graphe est symétrique par rapport à l’origine.

2. Limites
2.1. Définitions
Limite en un point

Proposition :

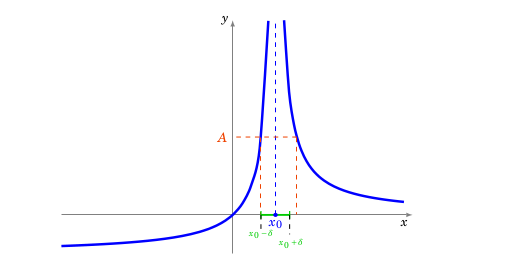
Limite en l’infini

Limite à gauche et à droite Soit $f$ une fonction définie sur un ensemble de la forme $]a, x_{0}[ ∪ ]x_{0} , b[$.

2.2. Propriétés

On a aussi

Ce sont des propriétés que l’on a l’ habitude d utiliser !

Enfin voici une proposition très importante qui lie le comportement d’une limite avec les inégalités.

3. Continuité en un point
3.1. Définition

3.2. Propriétés
La continuité assure par exemple que si la fonction n’est pas nulle en un point (qui est une propriété ponctuelle) alors elle n’est pas nulle autour de ce point (propriété locale). Voici l’énoncé :

La continuité se comporte bien avec les opérations élémentaires. Les propositions suivantes sont des conséquences immédiates des propositions analogues sur les limites.

La composition conserve la continuité (mais il faut faire attention en quels points les hypothèses s’appliquent).

3.3. Prolongement par continuité

4. Continuité sur un intervalle
4.1. Le théorème des valeurs intermédiaires

4.2. Applications du théorème des valeurs intermédiaires
Voici la version la plus utilisée du théorème des valeurs intermédiaires.
Corollaire 1
Soit $f : [a, b] → R$ une fonction continue sur un segment.

Démonstration
Il s’agit d’une application directe du théorème des valeurs intermédiaires avec $y = 0$. L’hypothèse $f (a) · f (b) < 0$ signifiant que $f (a) $et $f (b)$ sont de signes contraires.

Attention ! Il serait faux de croire que l’image par une fonction $f$ de l’intervalle $[a, b]$ soit l’intervalle $[ f (a), f (b)]$.

4.3. Fonctions continues sur un segment

Comme on sait déjà par le théorème des valeurs intermédiaires que f ([a, b]) est un intervalle, le théorème précédent signifie exactement que

Donc m est le minimum de la fonction sur l’intervalle $[a, b]$ alors que M est le maximum.
5. Fonctions monotones et bijections
5.1. Rappels : injection, surjection, bijection
Dans cette section nous rappelons le matériel nécessaire concernant les applications bijectives.

5.2. Fonctions monotones et bijections
Voici un résultat important qui permet d’obtenir des fonctions bijectives.

En pratique, si on veut appliquer ce théorème à une fonction continue $f : I → R$ , on découpe l’intervalle $I$ en sous-intervalles sur lesquels la fonction $f$ est strictement monotone.